ArithmerBlog 本スライドは、当社と国立大学法人東京大学との間の共同研究に基づき、2018年11月20日、同大 学大学院数理科学研究科・理学部数学科において開催された離散数理モデリングセミナーに甘利俊 一博士を招請するにあたり、事前の知識習得のために行った社内講義資料を公開用に一部修正したものです。
■目次
- ガウス分布の幾何構造
- 指数型分布族
- 双対平坦空間
■ガウス分布の幾何構造
■𝜇, 𝜎空間はユークリッド空間?
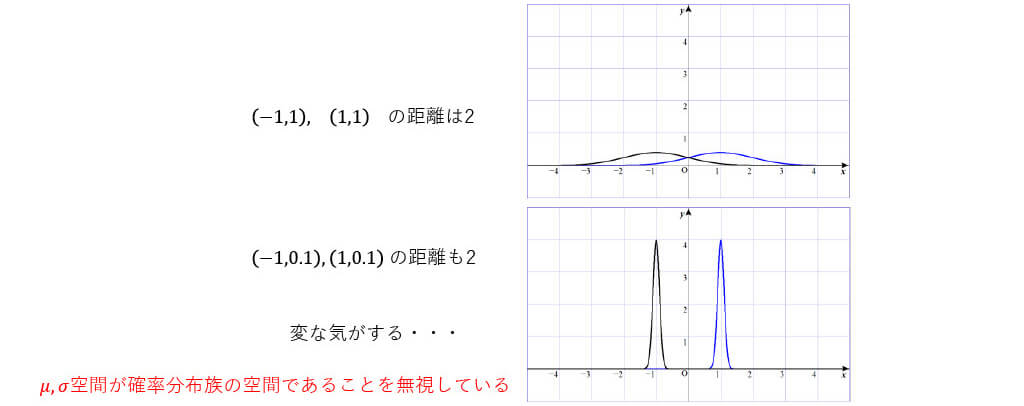
■𝜇, 𝜎空間のリーマン計量
■Fisher情報行列
■ガウス曲率
■𝜇, 𝜎空間のガウス曲率
■ガウス分布間の距離
■Kullback–Leiblerダイバージェンス
■ガウス分布間のKLダイバージェンス
■指数型分布族
■指数型分布族の性質
■指数型分布族の双対座標系
■指数型分布族のKLダイバージェンス
■𝜙( 𝜂) に関するBregmanダイバージェンス
■𝜽座標系と𝜼座標系の直線
■指数型分布族の幾何構造
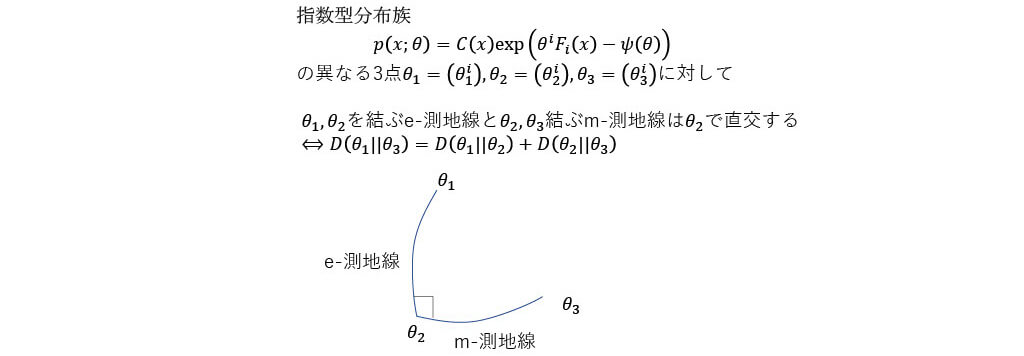
■双対平坦空間上のピタゴラスの定理
■参考文献
- Amari, S. Information Geometry and Its Applications (Applied Mathematical Sciences); Springer, 2016.
- 甘利俊一; 長岡浩司; 情報幾何の方法; 岩波書店, 1993.
- 藤原彰夫 情報幾何学の基礎; 牧野書店, 2015.
- Amari, S. Information geometry of the EM and em algorithms for neural networks; Neural Networks 1995, 8, 1379-1408
