私の趣味はオーケストラの一員としてヴァイオリンを演奏する事である。
先日ロシアの作曲家チャイコフスキーのオペラ『エフゲニー・オネーギン』を演奏する機会があった。この作品の原作は同じくロシアを代表する文豪の一人プーシキンの韻文小説である。
チャイコフスキーはオペラを作り上げたのだが、一方で(これまたロシアの)数学者マルコフはこの小説を研究対象として現代数学において極めて重要な分野の一つであるマルコフ過程論を発展させた。
恥ずかしながらオペラ『エフゲニー・オネーギン』を演奏するまで、それが仕事で使っているマルコフ過程論と間接的にせよ繋がりを持っていることに気づかなかった。
音楽とは人間の感情を揺さぶるように音を並べたものである。
「音から構成される音楽」と「物理現象として音を記述する数学」の間には、より直接的な関わりがあることは言うまでもない。しかし音楽と数学の関係を一つのブログ記事で網羅しようとするのは無謀な挑戦であろう。
今回は極めて入門的な内容にとどめ、前提知識として高校程度の数学を知っていればおおよそ理解できるように努める。
音は物理的には空気の振動(粗密波)で、時間tにおいてA sin(2πft)…①と書ける。
ここでA > 0は音の大きさ、すなわち音量に対応するパラメータ(物理学用語では振幅)、f > 0は音の高さ、すなわち音程に対応するパラメータ(物理学用語では周波数・振動数)である。
音量、音程に加えて音を特徴付けるもう一つの重要な要素は音色である。
実は音の記述①は不完全で、より一般にはフーリエ展開で表現する方がよく、その展開係数の比が音色に対応する。この記事ではそこまでは深入りせずに音は①で書かれることを前提とする。
手始めにパラメータの変化と人間が感じる音の変化を対応させてみよう。
Aが値として大きければ大きい程、音量は大きくなる。
同様にfが値として大きければ大きい程、音程は高くなる。
なお人間の可聴領域はf=20Hz~20kHz程度であるが、年齢と共に高周波音を捉える能力が衰えて行くことが知られている。いわゆるモスキート音を利用して「若者のたむろ」対策が行われているという話を聞いたことがあるかもしれない。
次に単一音ではなく、二つの音A1sin(2πf1t)とA2sin(2πf2t)の関係について考えてみよう。
f1 = f2の場合、二つの音程は一致していることになるが、実際には完全にf1= f2となることはあり得ない。f1とf2が同じではないが近い値を取るとき、うなり、すなわち合成音の大きさの周期的な変化が生じる。その周波数は|f1 – f2|となる。(演習問題:A1 = A2として三角関数の合成によってこの事を確認せよ。)例えばある楽器奏者1の音程f1を固定し、別の楽器奏者2は調律を行う状況を考える。
この際、楽器奏者2はうなり聞いてその周波数が出来る限り短くなるように、すなわち周波数の逆数である周期が出来る限り長くなるように音程f2を変化させている。
f1は実際の楽器でなく、電子音であってもよく、通常弦楽器または管楽器の調律はラの音またはシ♭で行う。「ラの音」と書いてしまったが、f = 440Hz程度の音のことをラと呼ぶ。
最近テレビの方ではなくなってしまったが、NHKラジオの時報は440Hzを用いている。
一方日本のオーケストラではf = 442Hzとするのが一般的である。
二つの周波数の比f2/f1のことも音程と呼ぶことがある。
カラオケで自分の声の音域に合わせてキーを変えるとはどういうことだろうか?
譜面上では音符の相対的な位置を変えずに全体を上下にシフトさせているだけである。
例えば、「ソ、ラ、シ」というメロディーの一部を全音下げると「ファ、ソ、ラ」となる。
数学的(物理学的)には周波数を上げ下げしているのだが、その際前の音との音程は維持される。
さて名前の付いている音程で一般にも有名なのはオクターブだろう。
f2/f1 = 2の時、f1とf2はオクターブの関係にあると言い、二つの音は同じ階名で呼ばれる。
例えば440Hzがラであれば、1オクターブ高い880Hzもラであるし、1オクターブ低い220Hzもラである。また周波数比が2 n(n:整数)の場合、nオクターブの関係にあると言い、やはり同じ階名が付けられる。
ピアノの鍵盤をイメージしてみよう。
1オクターブ間には白鍵と黒鍵合わせて11個の音が並んでいる。
例えばド(図上で左側のド)と「高いド」(図上で右側のド)の間にはド♯(レ♭)、レ、レ♯(ミ♭)、ミ、ファ、ファ♯(ソ♭)、ソ、ソ♯(ラ♭)、ラ、ラ♯(シ♭)、シがある。
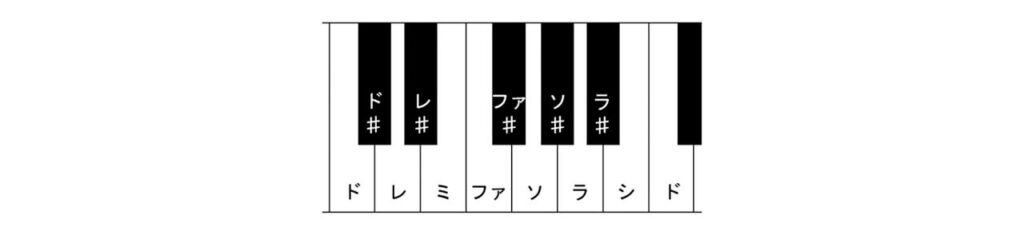
これらの音たちが、カラオケのキーチェンジのところで述べた性質を厳密に持つと仮定しよう。
例えば
f(レ)/f(ミ)=f(ファ)/f(ソ) 、f(レ)/f(ソ)=f(ミ)/f(ラ) 、f(ド)/f(ド♯)=f(レ)/f(レ♯)=f(ソ)/f(ソ♯)
ここでf(X)は階名Xに対応する周波数である。
満たして欲しいこの性質を一般的に書くと、
X-Y=Z-W に対してf(X)/f(Y)=f(Z)/f(W)…② となる。
ただしX-Yは、XがYより高い場合XとYの黒鍵と白鍵の数+1すなわち距離、
XがYより低い場合X-Y=-(Y-X)と定義する。
境界条件f(高いド)/f(ド)=2を満たす一意な解は簡単で、f(ド)を基準として
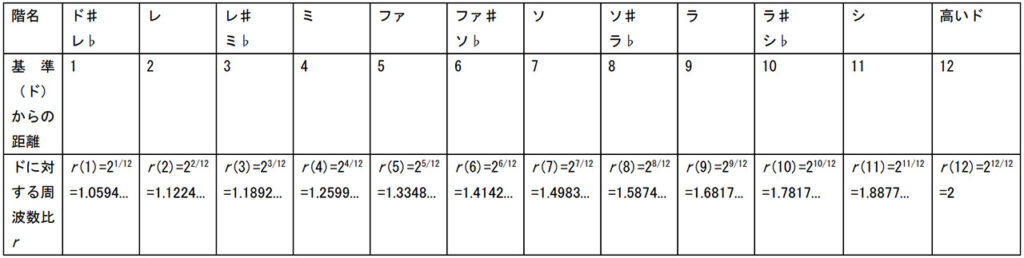
となる。
なおf(ラ)=440Hzとなるようにするには、f(ド)=261.63Hz程度である。
ピアノの鍵盤全域に拡張すれば任意の階名Xに対してf(X)/f(ド) =2( X-ド)/ 12となる。
このようにすべての音程が21/12のべき乗となる。
実際ピアノの調律ではこの音程が用いられている。
これでめでたく話が完結するかと思いきや、そうではない。
この「音律」は平均律と呼ばれ、よくできた定義の一つに過ぎない。
歴史的には平均律よりも先に純正律が用いられていた。
上記の表の通り、平均律では2以外の音程は全て無理数であるのに対し、純正律の音程は全て有理数である。
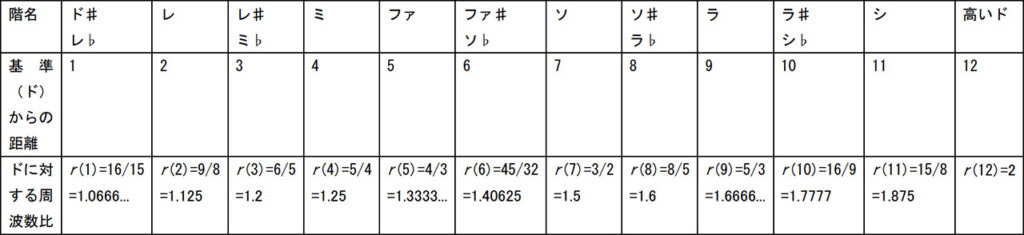
平均律は旋律(メロディー)向け、純正律は和音(ハーモニー)向けと言われることがしばしばある。例えば「ドミソ」の長三和音(明るく感じられることが多い和音)を考えてみよう。
平均律での周波数比は1:24/12:27/12となり、うなりが生じる。
純正律での周波数比は4:5:6となり、極めて正確に音程を取る技術がある楽器奏者や電子音で和音を奏でれば、うなりは生じずに澄んだ響きとなる。
ミを♭にした場合は短三和音(暗く感じられることが多い和音)である。
やはり平均律では無理数比1:23/12:27/12、純正律では整数比10:12:15となる。
純正律の場合、②は部分的、近似的にしか満たされない。
例えば、r(7)/r(3)=r(6)/r(2)=r(4)/r(0)=5/4=1.25であるが、r(8)/r(4)=32/25=1.28≒1.25となる。
また基準の音をどれに取るかによって、同じ階名でも周波数が異なってくる。
この記事では平均律と純正律を取り上げたが、それ以外にもピタゴラス音律など様々な音律が知られている。更に、そもそもオクターブを12分割しない方法(例えばインドネシアのガムラン)も存在する。それにも関わらず、たくさんの可能性の中からオクターブを12分割する方法が世界のスタンダードとなったのはなぜか?単なる偶然か?それとも人間の脳の性質として、何か特別な心地よさを感じるのだろうか?この問いに対する論理的な答えを少なくとも私は知らない。
この記事を書いた人

Arithmer CTO補佐 有田 親史
東京大学
理学系研究科物理学専攻修了(理学博士)。
九州大学、フランス・サクレー研究所、
ドイツ・ザールラント大学にて研究と教育に従事。
その後、直接社会と触れ合え自分の能力を生かせる場を求めて、2018年Arithmer入社。Arithmer CTO補佐に就任。
日本物理学会若手奨励賞受賞。
 ArithmerBlog
ArithmerBlog 
