~ トポロジーとパーシステントホモロジー ~
はじめに
物体をスキャンするなどして得られた 3次元の点群から、もとの物体のかたちに関する情報を得るために、さまざまな方法が用いられます。
例えば、Arithmer では
3Dビジョンロボットシステムなどで、 次元の点群を扱っています。
今回は点群から計算される情報として、近年注目を浴びているパーシステントホモロジーという概念を紹介したいと思います。
トポロジーという数学の一分野の考え方を使っているのですが、わかりやすさのために、ところどころで数学的に正確ではない表現をする事をお許しください。
「かたち」とは?~トポロジーの考え方~
ものの「かたち」とは何でしょうか? 例えば、丸と四角はかたちが違う、といいますよね。
それでは、こちらの図をみた時に、どれが丸でどれが四角でしょうか?
一番左は丸、一番右は四角だけど、左から二番目は丸のような四角のような、みたいな気持ちになりませんか?

トポロジー(位相幾何学)という数学の分野では、かたちに関してもっと雑な分類をします。
上の例のような、連続的に変形してうつりあうものは、全部同じかたちをしていると考えるので
す。今回は、このようなものたちを「位相的に同じかたち」をしていると呼ぶ事にします。
(本当は、連続的な変形以外でも位相的に同じかたちだと考えるものがあるのですが、今日は割愛させてもらいます。)
では、どういうものは違うと考えるのかというと、例えば、下の図の円盤と穴の空いた円盤は、(お互いを連続的に変形してもうつりあわないので)違うかたちをしていると考えます。

これは円盤じゃなくて四角ではないか? と思う方もいるかもしれませんが、先ほど述べたように、トポロジーの考え方では連続的に移り合うものは同じかたちだと思うので、一見四角く見えるこれらを円盤と呼んでしまうのです。
3次元空間の中の例も挙げておきます。
トポロジーの考え方では、球と四面体の表面はおなじかたちで、ドーナツの表面(トーラスと呼びます)は違うかたち、だと考えます。

かたちを見分ける ~ 位相不変量 ~
先程、上の図の、円盤と穴の空いた円盤は位相的に違うかたちをしていると言いましたが、本当は、どうやって連続的に変形してもお互いが移り合わないということを証明しないといけません。
では、二つのものが、位相的に違うかたちをしているというのは、どうやったらわかるでしょうか?
例えば、境界の数、というのは連続的に変形してもかわりません。そのため、円盤の境界は1つ、穴の空いた円盤の境界は 2つ、という事から、この二つが位相的に違うかたちをしている事がわかります。

また、下の図のごちゃごちゃした図形が、上の図のどちらと位相的に同じか、というのは、実は境界の数を数えればわかります。

左の図形は境界が全部繋がっているので円盤と同じかたちで、右の図は境界が2つあるので、穴の空いた円盤と同じかたちです。
境界の数のように、位相的に同じかたちをしたものに対して、同じ値をあたえる量を「位相不変量」と呼びます。
オイラー標数
もう少し複雑な位相不変量を紹介します。
$2$ 次元の図形 $D$ があった時に、それをきれいに三角形に分割します。そして、その三角形の枚数 $f$ と、辺の本数 $e$ と、頂点の個数 $v$ から、
$$ \chi(D) = f – e + v $$ を計算します。この $ \chi(D)$ を $D$ のオイラー標数と呼びます。
それでは、球面 $S$ と、トーラス $T$ のオイラー標数を計算してみましょう。
球面は、位相的には四面体と一緒なので、四面体を使って計算してみます。
四面体は面が $4$ つ、辺が $6$ 本、頂点が $4$ つですから、$$\chi(S) = 4 – 6 + 4 = 2$$ となります。
トーラス $T$ は、四角形の上の辺と下の辺、左の辺と右の辺を張り合わせたものだと考える事ができます。
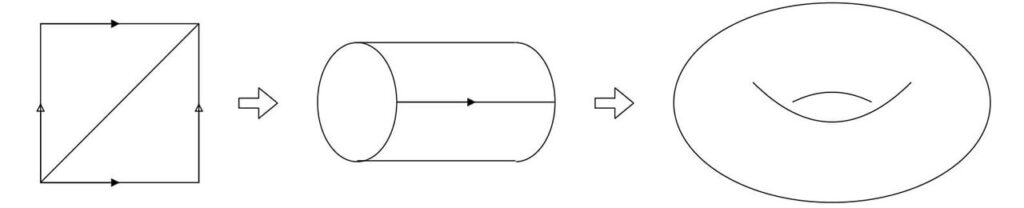
三角形の面が $2$ つ、辺は、上下の辺がくっついたものが $1$ 本、左右の辺がくっついたものが $1$ 本、対角線が $1$ 本で、合計 $3$ 本、頂点は、全ての頂点がくっついて $1$ つだけとなり、オイラー標数を計算すると以下のようになります。 $$\chi(T) = 2 – 3 + 1 = 0$$
オイラー標数が位相不変量である事を信じると、この計算から、球とトーラスが位相的に違ったかたちをしているという事がわかります。
ちなみに、トーラスのかたちをしている世界でもっとも有名なのが、ドラゴンクエストシリーズの世界ではないでしょうか。地図の上と下、左と右がくっついているということは、位相的にはトーラスであるという事なのです。
オイラー標数の位相不変性
オイラー標数について、もう少し詳しく見ておきましょう。
最初に不安になる事は、同じ曲面に対して、違った三角形分割をもってきたら、オイラー標数は違った値にならないでしょうか? という事ですが、実は大丈夫なのです。
その不変性について、一番本質的なところだけを紹介しましょう。
下の図の左、四角形を $2$ 枚の三角形で分割したものを考えると、$ f = 2, e = 5, v = 4 $ で $\chi = 2 – 5 + 4 = 1$ です。
図の右では、赤い頂点を追加して、それにともなって青い線が $2$ 本追加され、黒い線が二つに分割され、三角形は $4$ 枚になります。すると、やっぱり $\chi = 4 – 8 + 5 = 1$ です。

これを詳しく見てみると、ある辺に頂点を $1$ つ付け加えると、面が $2$ つ増え、辺が$3$ 本増えるので、足し引きするとちょうどキャンセルしてオイラー標数は変わらないのです。
実は、二つの三角形分割があった時に、このような操作を繰り返し行う事でお互いに移り合うという事が示せます。そのため、オイラー標数は三角形分割の取り方によらず、もとの図形だけから決まる量だという事がわかるのです。
さて、オイラー標数がきちんと定義されることがわかれば、それが位相不変量になっていることは、ほとんど明らかです。
$2$ つの図形が位相的に同じかたちならば、片方の図形にある三角形分割をそのままもう片方の図形に移す事ができます。その際に、三角形の枚数や辺の本数はかわらないので、オイラー標数もかわりません。
ホモロジー群
本題のパーシステントホモロジー群を説明するために、まず、ホモロジー群というものを紹介します。
ホモロジー群というのは、代表的な位相不変量のひとつです。つまり、位相的に同じかたちをしたものに対して、ある種の方法で定まる「群」です。
日本語での「群」は、「点群」のように、ある種のものの集まりをあらわす言葉なのですが、数学用語での「群」は「集合と演算を組にしたもの」だと思っておいてください。例えば「整数と足し算の組」や「実数上の全単射全体と写像の合成の組」などが群になります。
ホモロジー群では、集合として「空間上の道の集合」、演算としては「道の結合」を考えます。
ホモロジー群をきちんと説明しようとすると、さまざまな準備が必要となるので、今回は、一次元ホモロジー群 $H_1$ をいいかげんに紹介させてもらいます。
空間の上の道
まず、空間に対して「道」と呼ばれるものを雑に定義します。
空間 $X$ に対して、その上に基点 $x_0$ を一つ固定し、$x_0$ から出発して、$x_0 $ に戻ってくる経路を考えます。ただし、$X$ の中で連続的に移動させて同じになる経路は「同じ道」だと思う事にします。
そして、そのような道全体の集合を $ P (X) $ と書く事にします。
円盤の上の道の集合
まず、円盤 $D$ の場合に、道の全体の集合 $P(D)$ を考えてみます。
一番最初に考える道 $ e $ は、$x_0$ から出発して、ずーっと $x_0$ にいて、$x_0$ に帰ってくる道です。こういう、全く動かないものも道として考える事にします。
次に、図の赤い線 $ \alpha $ として、$ x_0$ を出発して、そこらへんを少し回って $x_0$ に戻ってくる道を考えます。
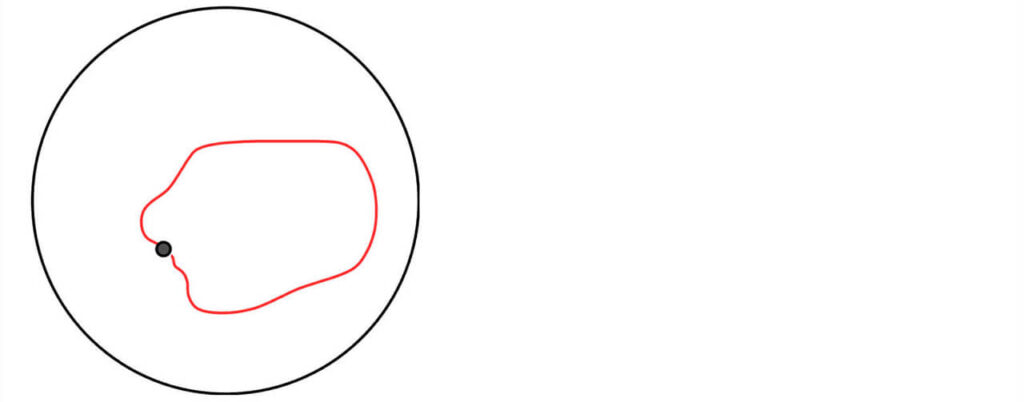
これは、$ e $ と同じ道でしょうか、違う道でしょうか?
円盤の上では、道を少しづつ連続的に移動させることで、どのような $\alpha$ に対しても、$ e $ まで変形する事ができます。
という事で、実は、円盤上には道は一種類しかなく、$ P (D) = { e } $ であるという事になります。
$P$ が $1$点集合の場合は演算を考える必要がないので、円盤 $D$ の一次元ホモロジー群 $H_1 (D) = { e }$ となります。
穴あき円盤の上の道の集合
その次に簡単な例を考えてみましょう。
$A$ として、円盤に穴を開けたものを考えます。$A$ 上の道として、赤い線を考えると、これは先程と同様に止まった道 $e$ と同じです。
ところが、青い線による道を考えると、この道はどのように変形しても円盤の穴に引っかかってしまうために、$e$ とは違う道だと考えられます。
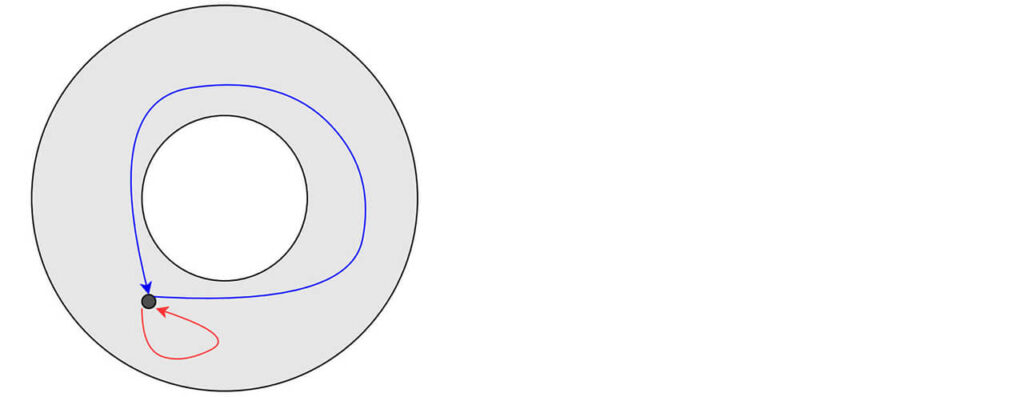
それでは、他にどのような道があるでしょうか?
例えば、赤い線を$2$回まわる道、逆向きに回る道などは、元々の赤い線とは違う道になります。一方で、どのような線を書いても、うまく変形すると、赤い線を何回かまわる道と同じであることが示せます。(証明はそれなりに大変なので割愛させていただきます)
つまり、$P(A) = { 赤い線を n 回まわる道 \mid n は整数 }$ となるのです。
この場合は、集合 $P$ と道をつなぐ演算を組にしたものが、一次元のホモロジー群 $H_1(A)$ となります。この群は、抽象的には整数全体のつくる群 $\mathbb Z$ と同じだとみなせるので、$ H_1(A) \cong {\mathbb Z}$ と書いたりします。
トーラスの上の道の集合
その次に複雑なケースがトーラス $T$ です。
$ e $ 以外の道として、まず思いつくのが、図に書いた赤い線 $ \alpha $ と、青い線 $\beta $ ではないでしょうか。
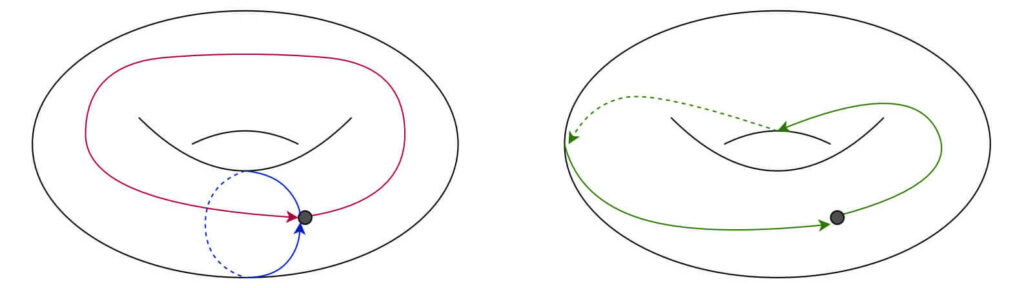
この $3$ つは、お互いにどうやっても連続的に移し合うことはできません。証明するにはそれなりに手間がかかるのですが、直感的にはほとんど明らかでしょう。
それ以外にどのような道があるかと言うと、たとえば、まず $\alpha$ を辿って、次に $\beta$ を辿るという道があります。これは、連続的に変形すると、緑で書いた $ \gamma $ という道になります。
では、先に $\beta$ を辿って、次に $\alpha$ を辿るとどうなるでしょうか? 実は、これも連続的に変形すると $ \gamma $ という道になります。
実は、トーラスの場合は、いくつかの道を順番に辿ったときにできる新しい道は辿る順番によらずに決まるので、新しい道 $\gamma$ を足し算の記号を使って $ \gamma = \alpha + \beta = \beta + \alpha $ と書く事にします。
ドーナツの絵をみるとわかりにくいかもしれませんが、ドラクエの地図(を4倍にしたもの)をみると、どうやって連続的に動かせばいいか、すぐに理解できるのではないでしょうか。
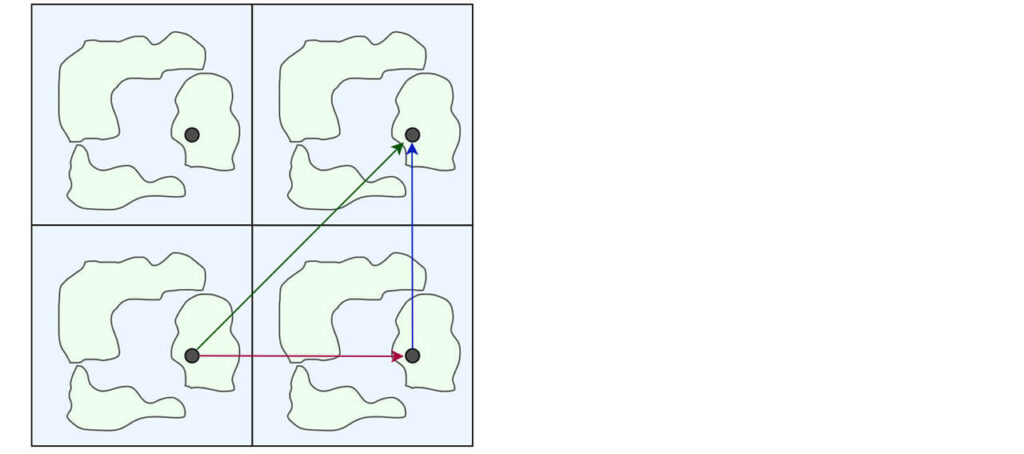
さて、これで、$ e, \alpha, \beta, \gamma $ の $3$ つの道があることがわかりました。それ以外にはどのような道があるでしょうか。たとえば、$ \alpha $ を2回辿る道、$ \alpha $ を逆方向に辿る道、$\alpha $ を $2$ 回と $\beta$ を $3$ 回辿る道、などなど、無限に思いつきます。
それらを合わせて考えると(証明は面倒なのですが)直感的には、トーラス上の全ての道の集合は、以下のようになる事がわかります。
$ P (T) = { a \alpha + b \beta \mid a, b \in \mathbb{Z} } $
ここで、道を繋ぐ演算を $+$ と書くことにしています。
この場合も $P$ に、道をつなぐ演算 $+$ を考えたものが、一次元のホモロジー群となります。数学っぽくいうと、$H_1(T) $ は、$2$ つの整数 $\mathbb{Z}$ の直積になります。
複雑な空間のホモロジー群と計算方法
今回は、これ以上複雑な場合に関しては深入りしませんが、一般の空間に対するホモロジー群では、道の集合の上の演算として、単に道をつなぐだけではなくて「つなぐ順番を入れ替えたものも同じ道だとみなす」という演算が必要になります。
また、実際にホモロジー群をどうやって計算するか、という事についても今回は触れませんが、空間の三角形分割があれば、そこからゴリゴリと計算する事ができるために、計算機上の計算とは相性が良いという事だけを述べておきます。
パーシステントホモロジー
与えられた点群に対して、ホモロジー群を使って特徴を捉えようという試みの一つが、パーシステントホモロジーという考え方です。
パーシステントホモロジー群の定義
与えられた点群を $P = { p_1, p_2, \cdots, p_n } $ とします。
正の整数 $d > 0$ に対して、三角形分割された空間 $X_d$ を以下で定めます。
- 点群のそれぞれの点に対して半径 $d$ の球を考えます。
- 点群の $2$ つの点 $p, q$ に対して、それらを中心とした球が交わっていれば、$p$ と $q$ の間に辺を引きます。
- 点群の $3$ つの点に対して、$3$ つの球に共通部分があれば、その $3$ 点でかこまれた領域に三角形を作ります。
このようにして、点群 $P$ に対して, 正数 $d$ を決めるたびに、三角形分割された空間 $X_d$ を作る事ができます。
この空間の $l$ 次元ホモロジーを $ H_l (X_d) $ とすると、$d$ を $d_0, d_1, d_2, \cdots $ と変えるにしたがって変化する $l$ 次元ホモロジー群の列 $ H_l(X_{d_0}), H_l(X_{d_1}), \cdots $ が得られます。
これを $l$ 次元のパーシステントホモロジー群と呼びます。
具体例
それでは、簡単な例を計算してみましょう。
下の図は $P$ として $8$ つの点を考えて、左から、$d =d_1, d_2, d_3, d_4$ と少しずつ半径を大きくしていった図です。
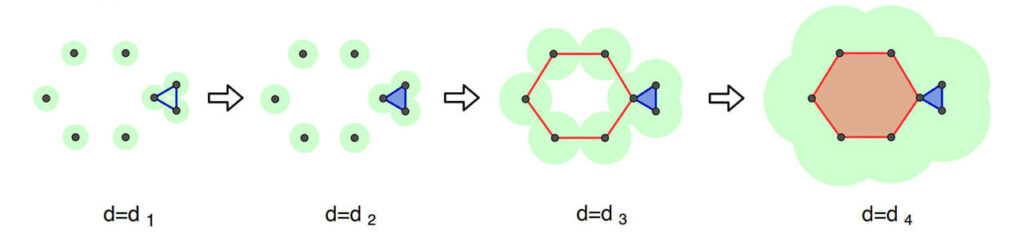
$d=d_1$ では、右側の $3$ つの点を中心とした円が互いに重なり、$3$ 本の辺ができます。これは、位相的には穴のあいた円盤と同じかたちで、道全体の集合は、青の線を何回まわるかだけで記述でき、$H_1(X_{d_1}) \cong \mathbb{Z}$ となります。時間 $d=d_1$ で、新しいホモロジー元として青の道が誕生した、と考える事ができます。
$d=d_2$ では、右側の $3$ つの点を中心とした円が $3$ つ同時に重なり、三角形が $1$ 枚できます。この時に、先ほどできた青の道は、ホモロジー元としては基点にずっと止まっている元 $e$ と同じになるため、ホモロジー元としては消滅したと考える事にします。
$d=d_3$ では、左側の $6$ つの点を中心とした円が互いに重なり、赤の線でできた道が新しいホモロジー元として誕生します。
$d=d_4$ まで進むと、左側に六角形ができ、赤の道はホモロジー元としては消滅します。
パーシステント図
パーシステントホモロジー $ H_1(X_{d_1}), H_1(X_{d_2}), \cdots $ に対して、その生成元の発生と死滅の時間をプロットしたものを、パーシステント図と呼びます。
先程の例に関してのパーシステント図は以下のようになります。

青い線に対応するホモロジー元は対角線に近い部分にありますが、これは生成してすぐ死滅するホモロジー元事をあらわします。
一方、赤い線に対応するホモロジー元は対角線から比較的遠い部分にありますが、これは長い時間安定して存在してる事をあらわし、点群の大域的な構造に対応すると考えられます。
このように、点群に対してパーシステントホモロジー群とパーシステント図を計算すると点群の構造に対するある種の情報が得られる事になります。
おわりに
今回の記事では、パーシステントホモロジーを簡単に紹介させていただきました。
トポロジーという分野は、数学の中でもなかなか習わない分野なので、馴染みのない方が多いのではないかと思いますが、ちょっとでも興味を持っていただけたらありがたいです。
 ArithmerBlog
ArithmerBlog 
