弊社は「数学で社会課題を解決する」というミッションを掲げておりますが、その弊社内で数学を使って実際に課題解決の手助けになった話をしようと思います。

最近、弊社では社員の大半が移動することになる大規模な席替えが行われました。
ただフレックスタイム制を導入しているため、またコアタイムがあっても会議などで埋まってしまうため、席替えタイムを設けてみんなで同時に移動するといった方法がとれません。したがって各自、新しい席が空くタイミングを見計らって移動することになります。
座席は全部埋まっているわけではないので、移動先の席が最初から空席だった人はそこに移動すれば、その席に移動予定だった人は移動できるようになるわけです。
ただし
・Aさんは今Bさんが使っている席に移動する
・Bさんは今Cさんが使っている席に移動する
・Cさんは今Aさんが使っている席に移動する
というようなサイクルが発生していたならば、新しい席が空白になるタイミングがなくなってしまいます。
この例のように3人くらいなら話し合って時間を合わせて移動すれば解決できるかもしれませんが、10人くらいでこのような移動のサイクルができてしまったらそれも難しくなってきます。席替えのプランを聞いたとき、まずこのようなサイクルが出来ていないか疑問に思いました。紙に書いて確認するもよいのですが、これはコンピューターを使って簡単に計算できる問題です。
ここで必要な情報は「移動する人」と「移動先の席に今座っている人」の関係です。
この関係は必ずしも対称ではありません。すなわち、AさんはBさんの席に移動するけどBさんは必ずしもAさんの席に移動するわけではありません。このような関係を記述するのに有効な数学のツールとして有向グラフがあります。Aさんが今Bさんの座っている席に移動しようとしているなら、AからBに有向辺が存在するとして、A→Bと表すことにします。さらにBさんが今Cさんのいる席に移動しようとしているなら、A→B→Cとします。これを全ての移動する人と移動先にいる人の関係性をついて行っていくことで有向グラフが作成され、席替えの問題は「与えられた有向グラフにおいてサイクルが発生するか」という数学の問題に読み替えられます。
この問題はpythonのNetworkXというライブラリを使うと直ちに解決し、実際の座席移動関係をもとに作成したグラフは以下になります。
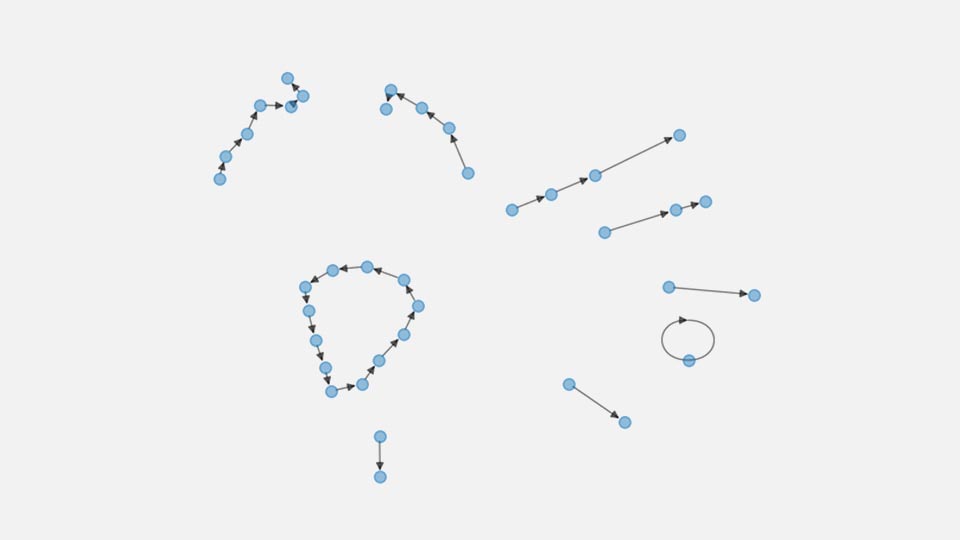
残念ながらサイクルが1つ発生してしました。しかも割と大規模なものです。
このグラフを社内で公開したところ、サイクルの中にいて当時別オフィスでの仕事が多かった一人が荷物をまとめてロッカーにしまってくれたおかげで座席が空き、サイクルが実質的に解消されました。また可視化により移動の指示を出しやすくなることにもつながりました。結果として座席移動の効率化がなされたことになります。
ソリューションを提供するというと、具体的にこうしなさいといったことまで提案しなければならないと思いがちですが(実際、そうできるのが理想だと思います)、このように適切な形で表示してそれを見てもらうだけでも、問題点が何かを共有できます。それにより、自分たちでは思い付かないような専門知識に基づいた解決法が提供されることもあるのだ、と考えさせられました。
以上、席替えという身近なところにも数学が活用できる場面があるという話でした。
 ArithmerBlog
ArithmerBlog 
