本資料は2019年8月8日に社内共有資料として展開していたものをWEBページ向けにリニューアルした内容になります。
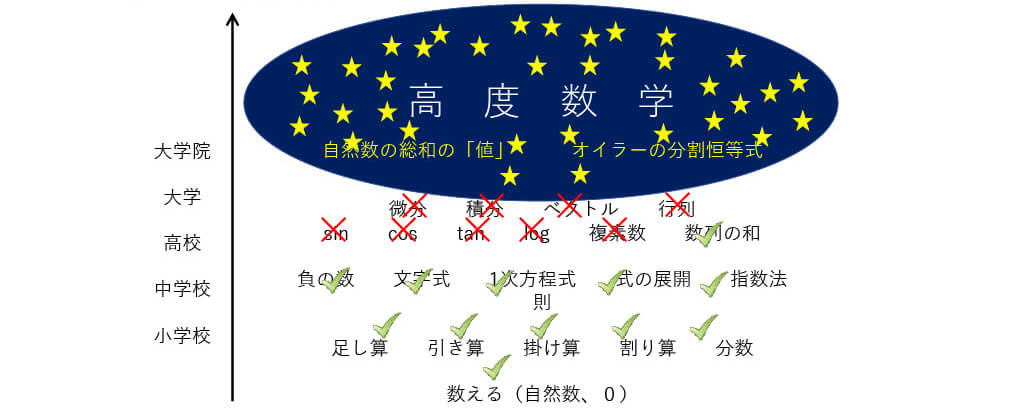
■高度数学は難しい

弊社は「高度数学」を活用したAI技術を生み出しています。
しかし高度数学を理解するのは一般には簡単ではないでしょう。
例えば上の本のあるページを見てみましょう。
小学生で習う足し算引き算から微分や行列といった事項を積み上げ式に習得しておかなければならないことに気付きます。
[I Goodfellow, Y Bengio, and A Courville: Deep Learning (2016)]
■今日の話題
今日のお話しでは、ちょっとずるをして、不思議な高度数学の世界を垣間見てみたいと思います。
ほんの少し算数の範囲を逸脱しますが、サインコサインも微分積分も使いません。
■自然数 1, 2, 3, 4, 5, …

■自然数の和
1 = 1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
1 + 2 + 3 + 4 + 5 = 15
1 + 2 + 3 + 4 + 5 + 6 = 21
1 + 2 + 3 + 4 + 5 + 6 + 7 = 28
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
■ピタゴラス学派の方法を使った計算
1 + 2 + 3 + 4 + 5 + … + 9 + 10 = 10×11÷2 = 55
1 + 2 + 3 + 4 + 5 + … + 99 + 100 = 100×101÷2 = 5050
1 + 2 + 3 + 4 + 5 + … + 2018 + 2019 = 2019×2020÷2 = 2039190
1 + 2 + 3 + 4 + 5 + … + 9999 + 10000 = 10000×10001÷2 = 50005000
問 1 + 2 + 3 + 4 + 5 + … = ?
■自然数の総和

■グランディ級数1−1+1−1+1−1+1−・・・

■交代級数(の一つ)1−2+3−4+5−6+7 ・・・

■ラマヌジャンによる「証明」

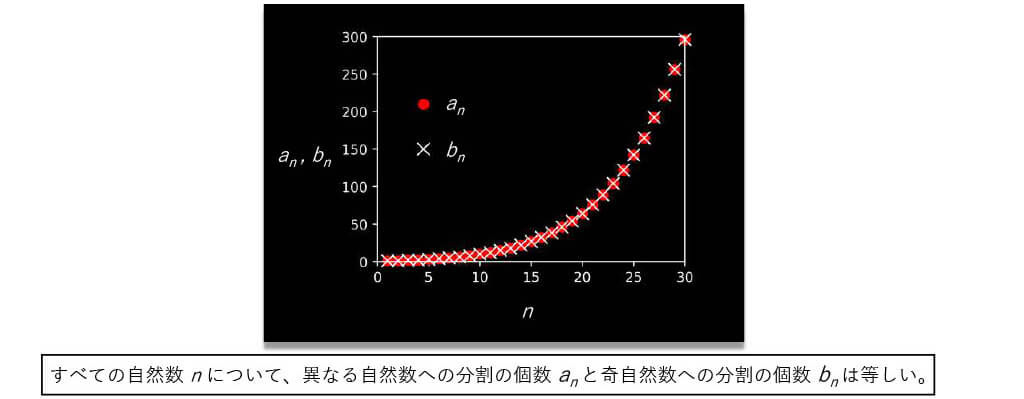
■自然数の分割
ある自然数n の分割とは、n をいくつかの自然数の和として書くことである。
(ただし大きい順に並べる。)
例えば
5 = 3 + 2
● ● ● | ● ●
10 = 6 + 2 + 1 + 1
● ● ● ● ● ● | ● ● | ● | ●
17 = 5 + 3 + 3 + 2 + 2 + 2
● ● ● ● ● | ● ● ● | ● ● ● | ● ● | ● ● | ● ●
■異なる自然数への分割

■異なる自然数への分割の個数 an

■奇自然数(2で割ると1余る自然数)への分割

■奇自然数への分割の個数 bn

■オイラーの分割恒等式
■オイラー

レオンハルト・オイラー (スイス)
- 解析、数論、幾何、理論物理に多大な影響を及ぼした。
- 分割恒等式以外にも「オイラー○○」を挙げる切りがない。
- オイラーの等式
- オイラーの一筆書き定理など。
- 両目の視力を失っても研究意欲が衰えることなく人類史上最も多くの論文を書いたとされる。
(5万ページ以上。)
関数の記法 $y=f(x)$ を導入。
■異なる自然数への分解の個数 anの母関数 A

■奇自然数への分解の個数 bn の母関数 B
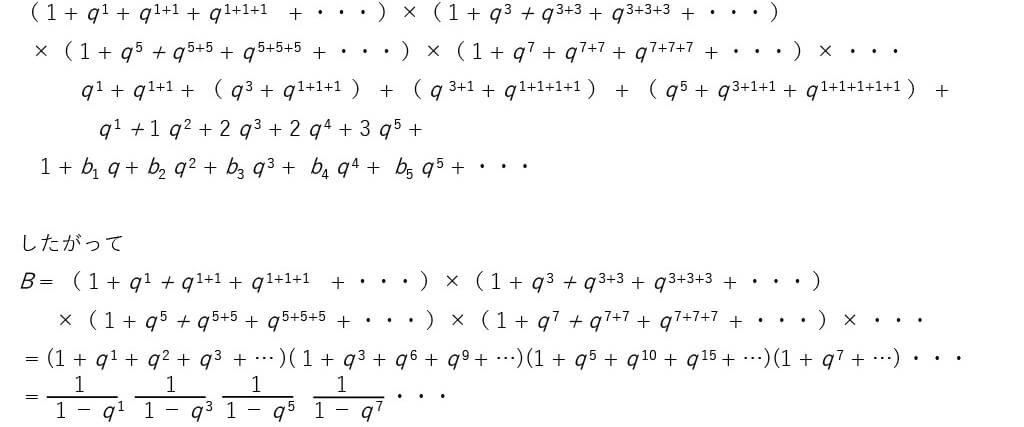
■分割恒等式 an = bn の証明
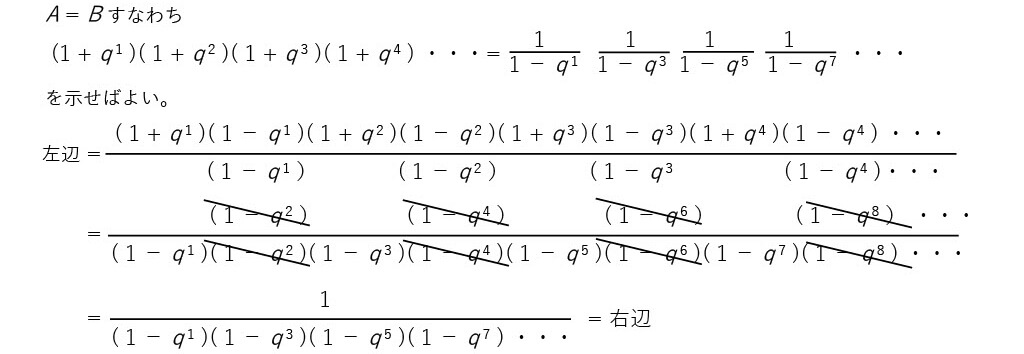
■まとめ
自然数の総和
$1+2+3+4+5+$…$=-\frac{1}{12}$
オイラーの分割恒等式
$a_n=b_n$
を証明しました。
 ArithmerBlog
ArithmerBlog