本資料は2019年9月12日に社内共有資料として展開していたものをWEBページ向けにリニューアルした内容になります。
■Purpose
Purpose of this material
- Overview of 3D deep learning
- Comparison b/w each method of 3D deep learning
- Main papers (In this material, I have summarized the material based on following materials and cited papers therein.)
■Application
Application of 3D Deep Learning

■Agenda
Methods of 3D Deep Learning
- Euclidean vs Non-Euclidean
- Euclidean Method
- Projections / Multi-View
- Voxel
- Non-Euclidean Method
- Point Cloud / Mesh / Graph
- Accuracy
- Dataset / Material
- Appendix
- Mesh Generation
- Laplacian on Graph
- Correspondence
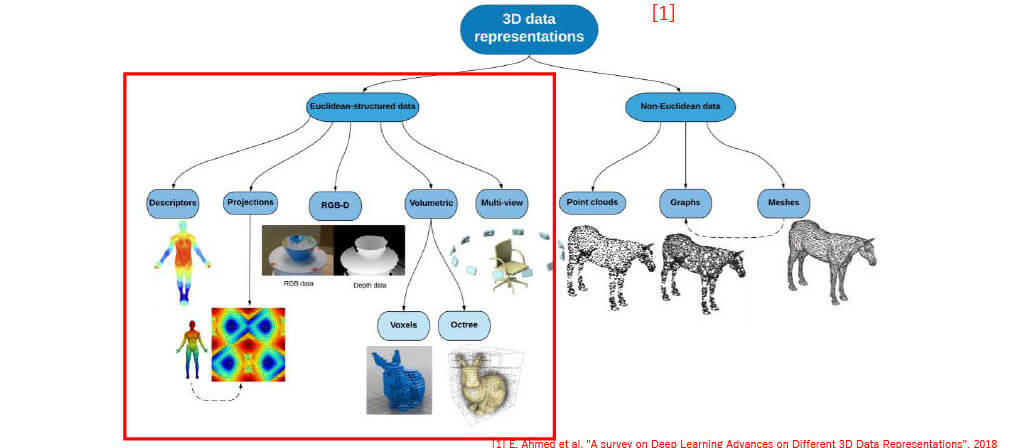
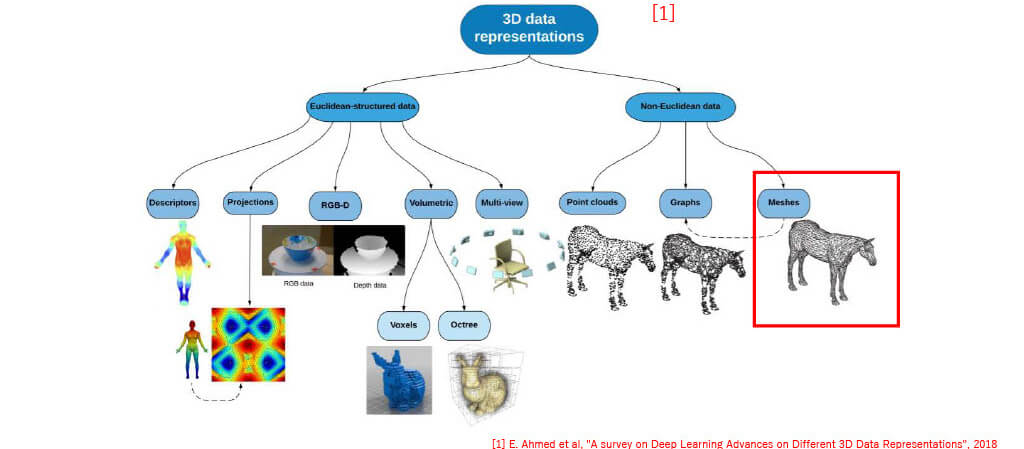
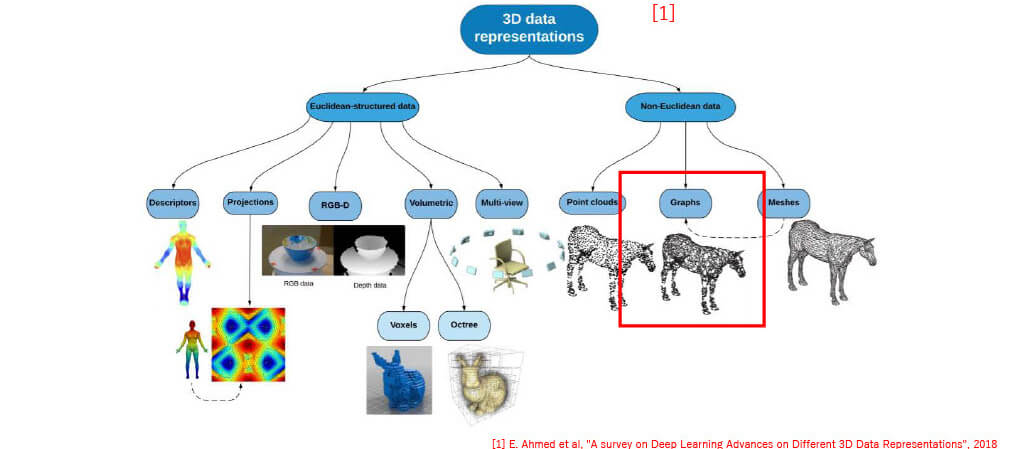
■3D Data
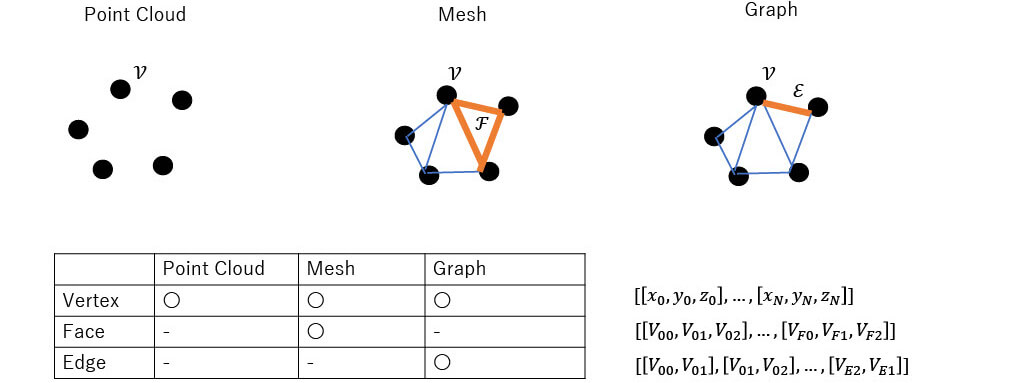
■Representation
Representation of 3D data
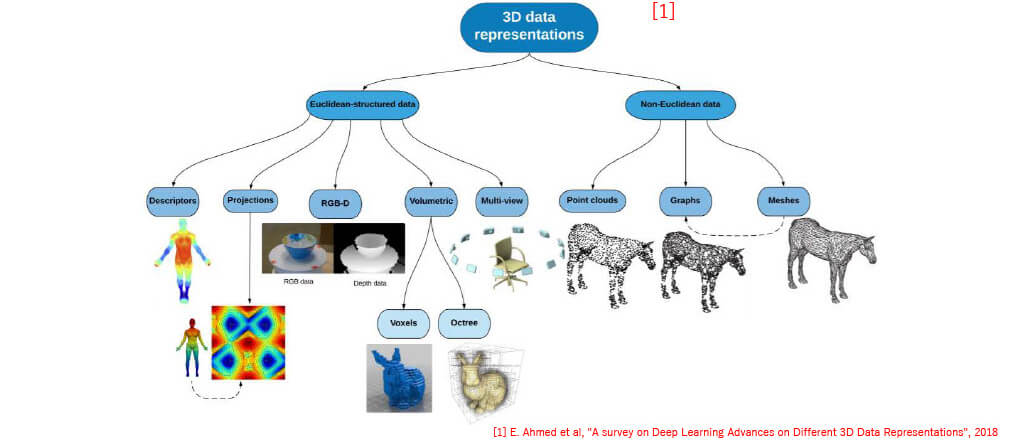

■Euclidean vs Non-Euclidean
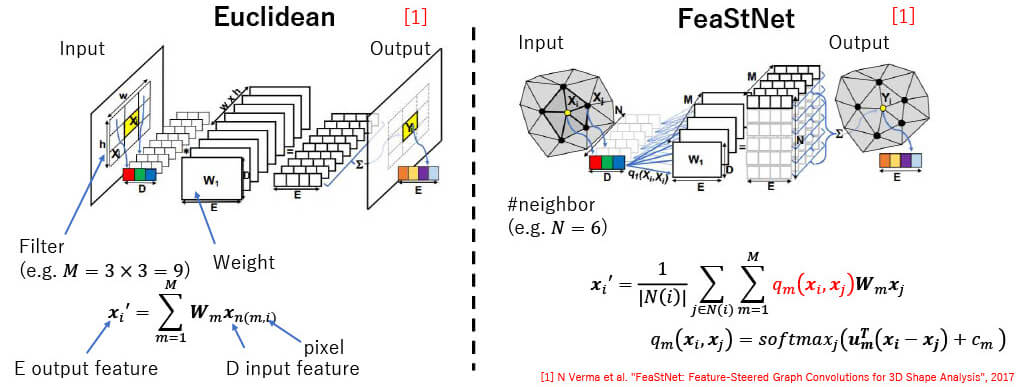
Euclidean
Euclidean (detail of feature)
Non-Euclidean
Non-Euclidean (detail of feature)
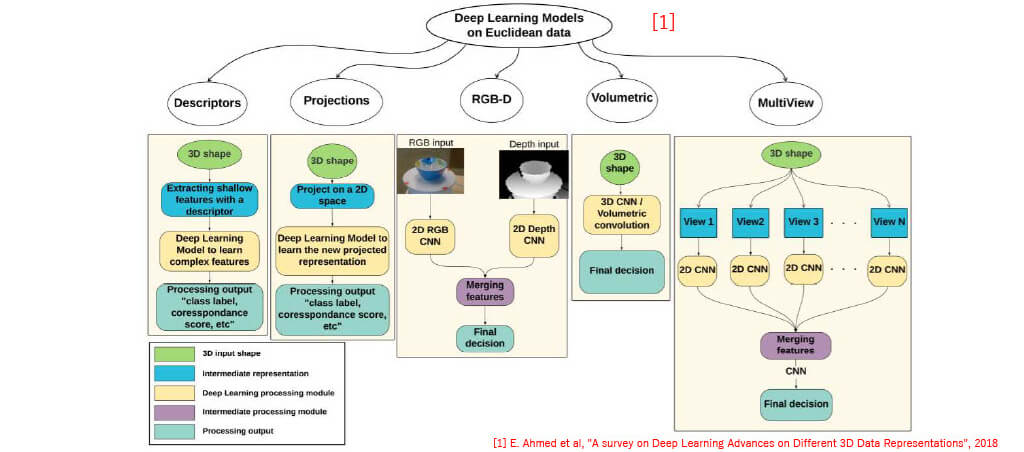
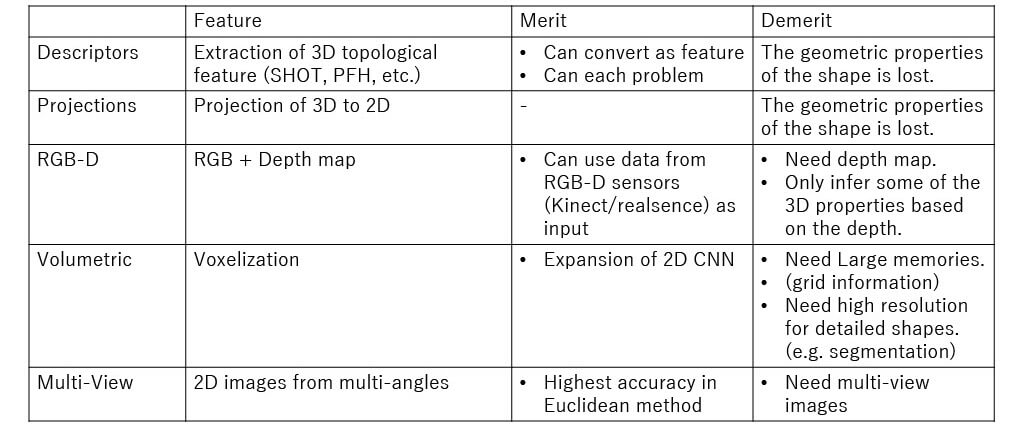
■Euclidean
Representation of 3D data
Each Euclidean Method (Projections / RGB-D / Volumetric / Multi-View)
| Method | Application | Link |
|---|---|---|
| Deep Pano | Classification | Link① |
| Two-stream CNNs on RGB-D | Classification | Link② |
| VoxNet | Classification | Link③ GitHub(Keras)① |
| MVCNN | Classification Retrieval | Link④ GitHub(PyTorch/TensorFlow etc.)② |
Deep Pano [1]
- Projection to Panoramic image
- Row-wise max-pooling for rotational invariant

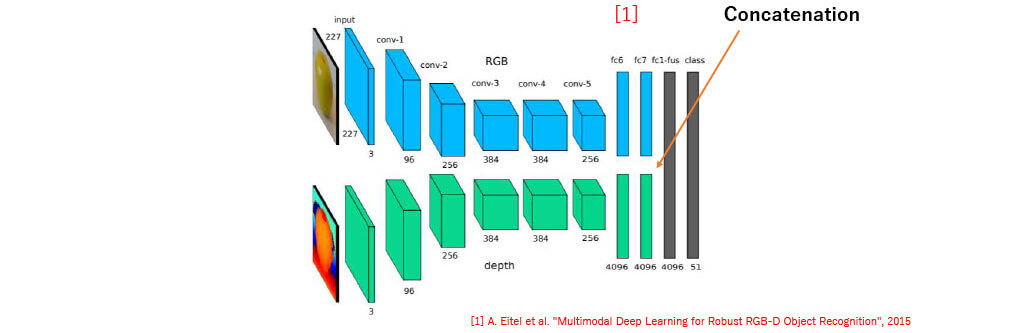
Two-stream CNNs on RGB-D [1]
- Concatenate CNN of RGB and CNN of depth map
VoxNet [1]
- Voxelization of 3D point cloud to voxel
- Not robust for data loss

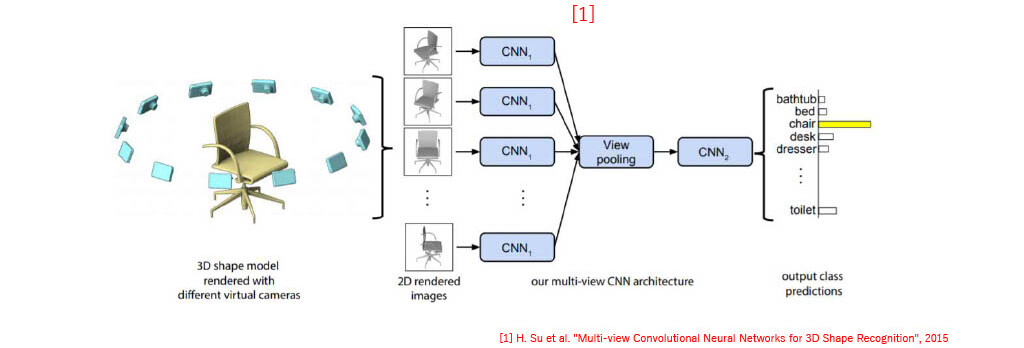
MVCNN [1]
- Merge CNN of each images
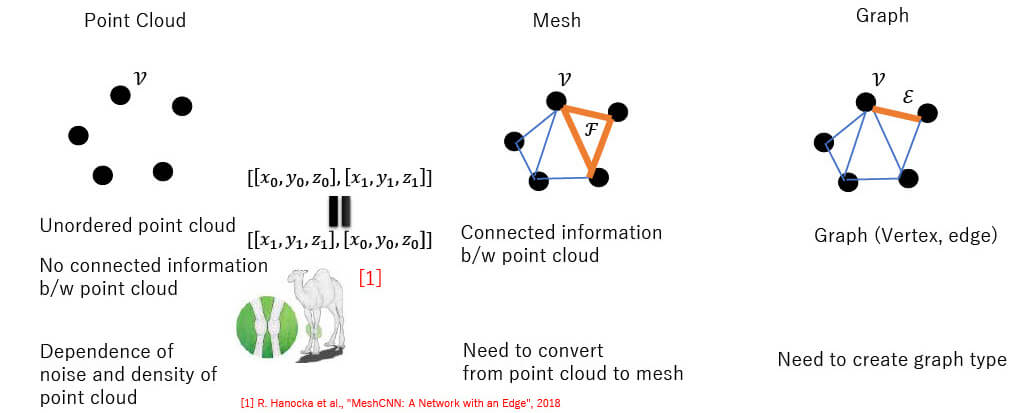
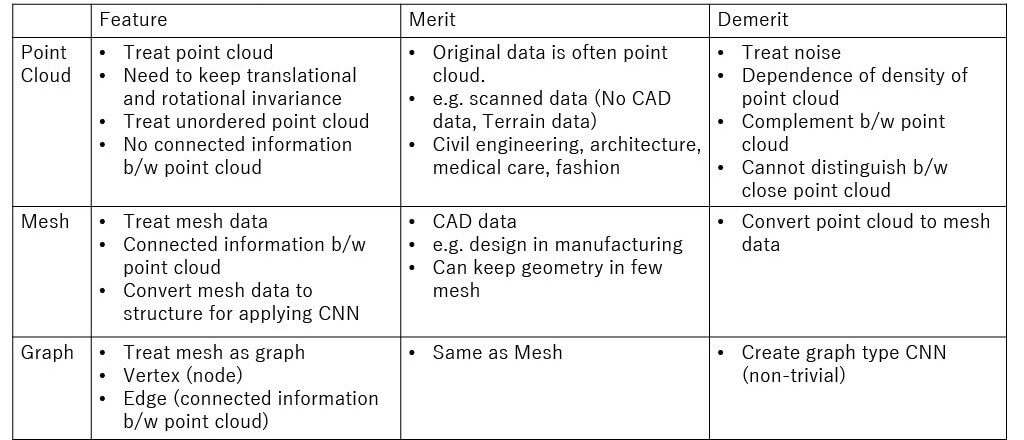
■Non-Euclidean (Point Clouds)
Representation of 3D data

Each Non-Euclidean Method (Point Cloud)
| Method | Application | Link |
|---|---|---|
| PointNet | Classification Segmentation Retrieval Correspondence | Paper GitHub (TensorFlow) |
| PointNet++ | Classification Segmentation Retrieval Correspondence | Paper GitHub (TensorFlow) PyTorch-geometric (PointConv) |
| Dynamic Graph CNN(DGCNN) | Classification Segmentation | Paper GitHub (PyTorch/TensorFlow) PyTorch-geometric (DynamicEdgeConv) |
| PointCNN | Classification Segmentation | Paper GitHub (TensorFlow) PyTorch-geometric (XConv) |
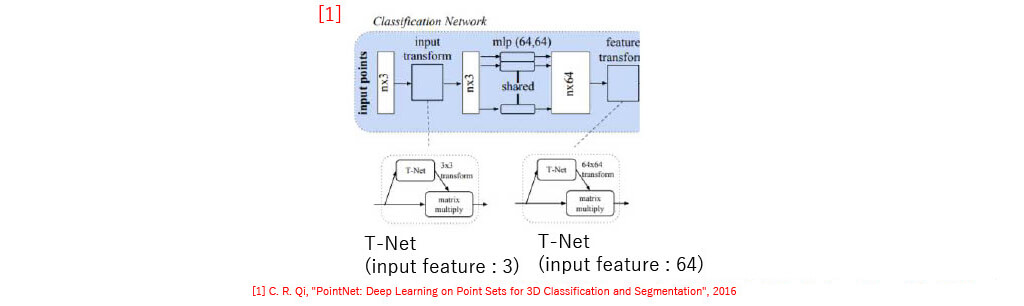
PointNet [1]

PointNet
T-Net [1]
- Similar to Spatial Transformer Networks in 2D
- Spatial Transformer Networks
- Alignment of image (transformation, rotation, distortion etc.) by spatial transformation
- Learn affine transformation from input data (not necessarily special data)
- Can insert this networks at each point b/w networks

| Reference | Contents |
|---|---|
| Paper | Original Paper |
| Sample(PyTorch) | Dataset : MNIST |

T-Net
- 3D ver. of Spatial Transformer Networks in 2D
- Not need sampling grid (There are no gird structure in 3D)
- Directly apply transformation to each point cloud
- Output parameter
- 3 × 3 in first T-Net
- 64 × 64 in second T-Net
PointNet++ [1]
- Comparison b/w PointNet
- Detailed information is kept
- Can treat different density of point cloud
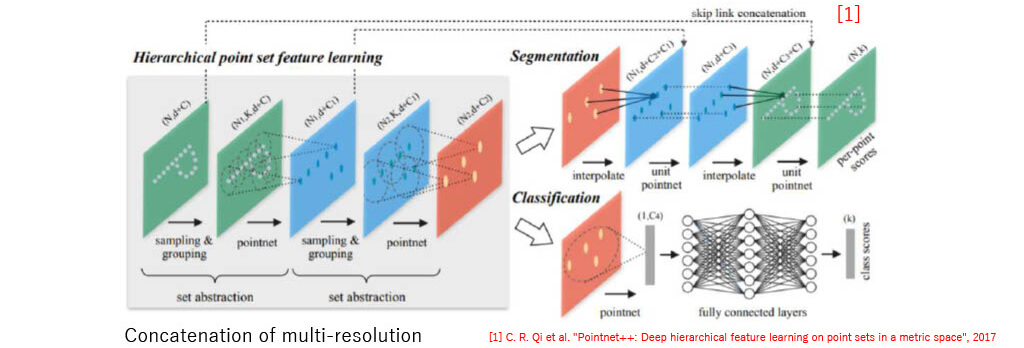
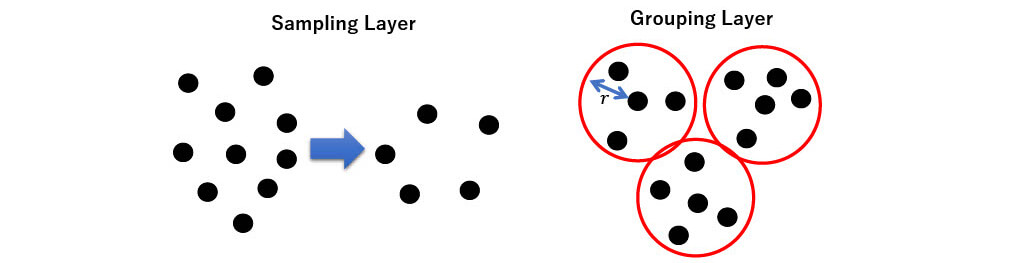
Set abstraction
- Grouping in one scale + feature extraction
- Sampling Layer : Extraction of sampling points by farthest point sampling (FPS)
- Grouping Layer : Grouping points around sampling points
- PointNet Layer : Applying PointNe
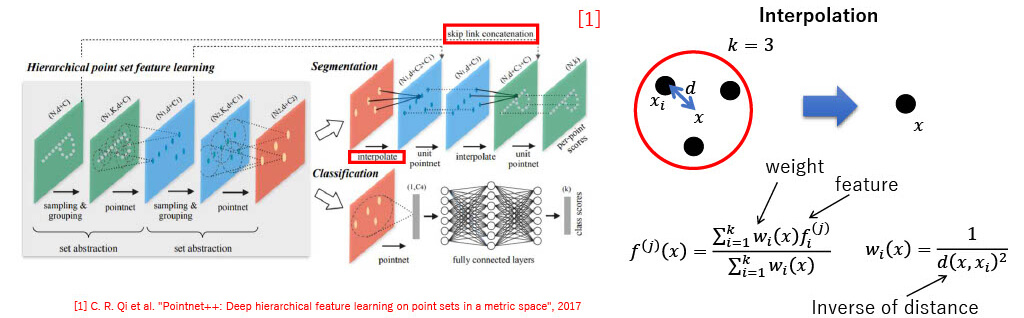
- Point Feature Propagation for segmentation
- Interpolation : interpolation from k neighbor points
- Concatenation
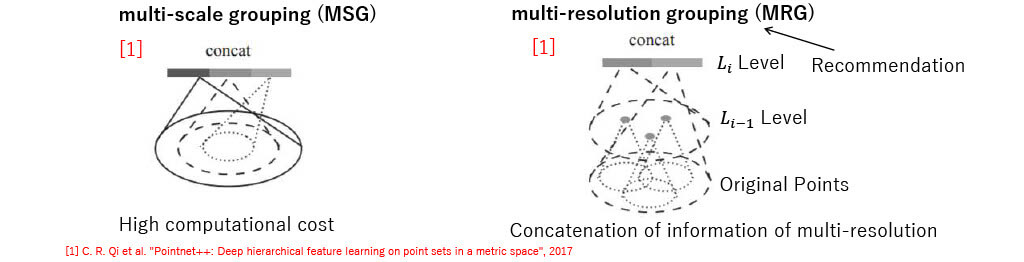
- Single scale grouping
- Multi scale/resolution grouping
- Combination of features from different scales
- Combination of features from different scales
- Modifying architecture in set abstraction level
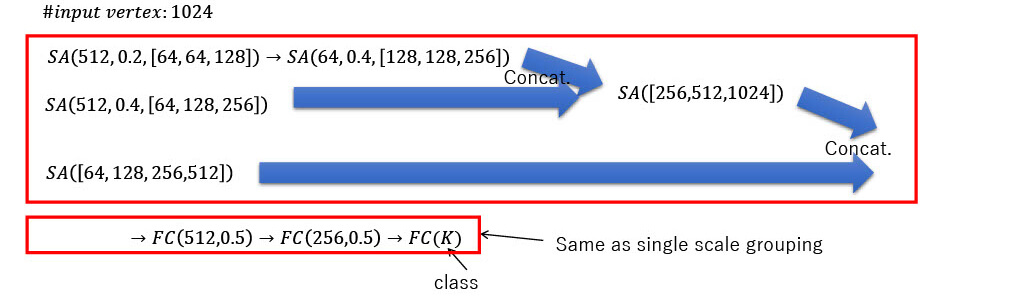
- Detail of architecture
- Note: #vertex is fixed
Architecture for classification and part segmentation of ModelNet using single scale grouping

- Detail of architecture
- Note: #vertex is fixed
Architecture classification of ModelNet using multi-resolution grouping (MRG)
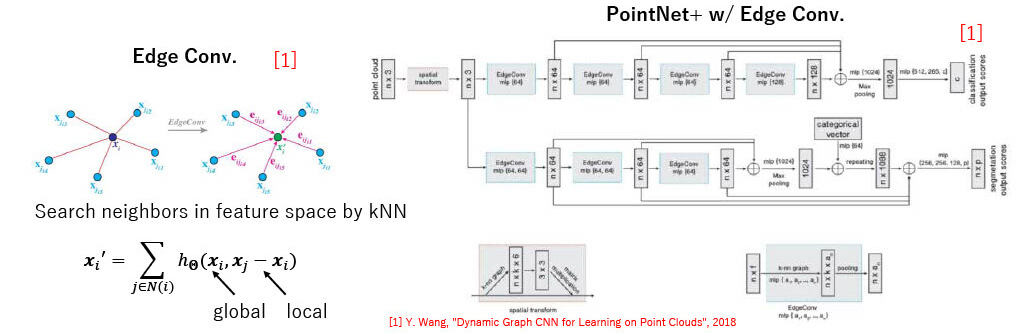
Dynamic Graph CNN (DGCNN) [1]
- PointNet + w/ Edge Conv.
- Edge Conv.
- Create local edge structure dynamically (not fixed in each layer)
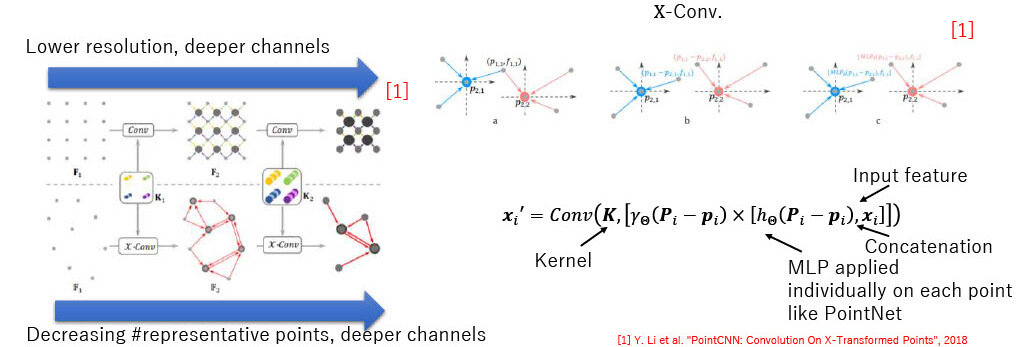
PointCNN [1]
Downsampling information from neighborhoods into fewer representative points
■Non-Euclidean (Mesh)
Representation of 3D data
Each Non-Euclidean Method (Mesh)
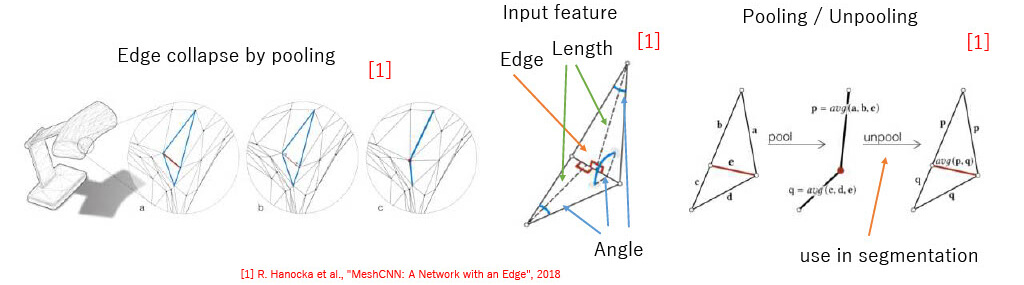
MeshCNN [1]
- Edge collapse by pooling
- Can apply only the manifold mesh
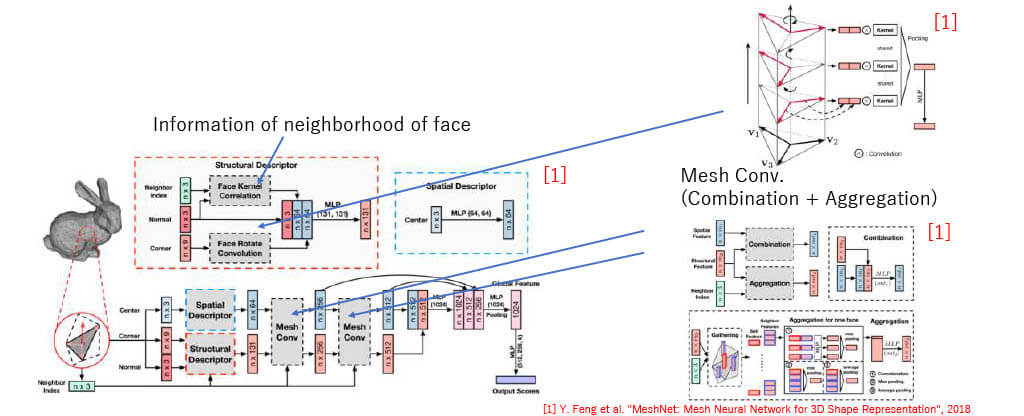
MeshNet
- Input feature
- Center, corner, normal, neighbor inde
■Non-Euclidean (Graph)
Each Non-Euclidean Method (Graph)
Spectral / Spatial Method
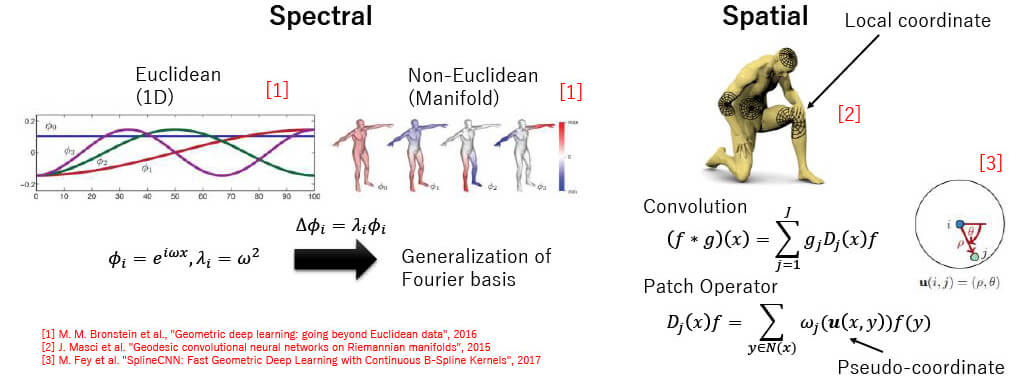
Each Non-Euclidean Method (Graph)
Spatial method is more useful than spectral method.

※Some equations from following pages are referred to the documents in PyTorch-geometric.
(https://pytorch-geometric.readthedocs.io/en/latest/modules/nn.html)
I will explain PyTorch-geometric in later page.
Each Non-Euclidean Method (Graph)
Spectral, Spectral free
Spectral CNN [2]
- cannot use different shape
- Spectral filter coefficients is base dependent
- High computational cost
- No locality

Chebyshev Spectral CNN (ChebNet) [1]
- Not calculate Laplacian eigenvectors directly
- Locality (K hops)
- Approximate filter as polynomial
Graph Convolutional Network (GCN) [2]
- Special ver. of ChebNet (𝐾 = 2)

Each Non-Euclidean Method (Graph)
- Charting
| Application | Link | |
|---|---|---|
| Geodesic CNN | Mesh Shape retrieval /correspondence | Paper |
| Anisotropic CNN | Mesh / point cloud Shape correspondence | Paper |
| MoNet | Graph / mesh / point cloud Shape correspondence | Paper PyTorch-geometric (GMMConv) |
| SplineCNN | Graph / Mesh Classification Shape correspondence | Paper GitHub (PyTorch) PyTorch-geometric (SplineConv) |
| FeaStNet | Graph / Mesh Shape correspondence Segmentation | Paper PyTorch-geometric (FeaStConv) |
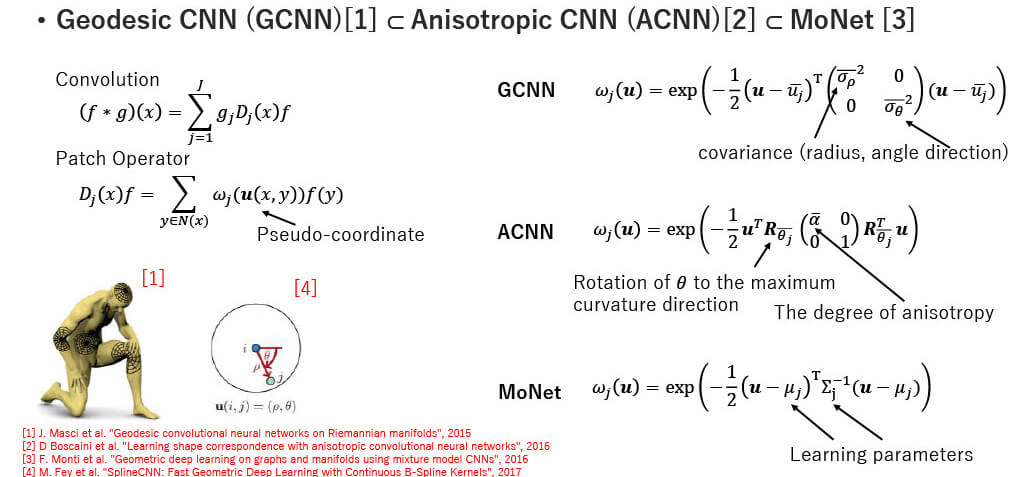
Geodesic CNN (GCNN)
- Create local coordinate
- Do not verify the meaningful chart (need to create small radius chart)
Anisotropic CNN (ACNN)
- Fourier basis is based on anisotropic heat diffusion eq.
MoNet
- Learn filter as parametric kernel
- Generalization of geodesic CNN and anisotropic CNN
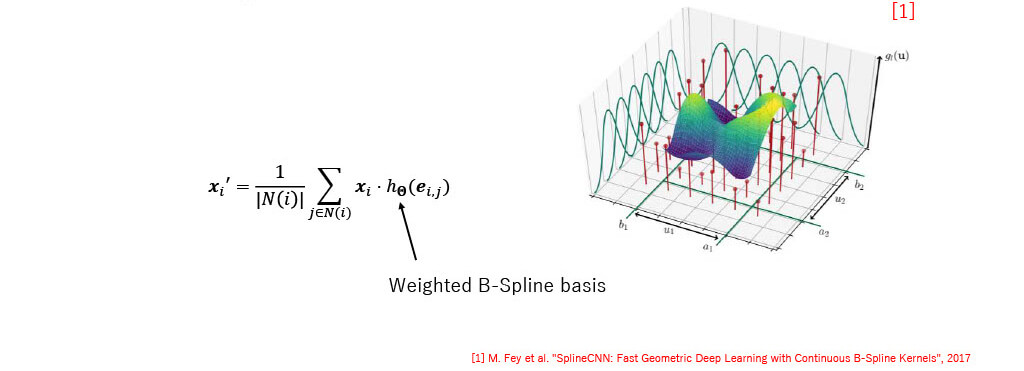
SplineCNN [1]
- Filter based on B-spline fun
FeaStNet [1]
- Dynamically determine relation b/w filter weight and local graph of a node
PyTorch-geometric

- https://github.com/rusty1s/pytorch_geometric
- Library based on PyTorchLibrary based on PyTorch
- For point cloud, mesh (not only graph)
- Include Point cloud, graph-type approach code
- PointNet++, DGCNN, PointCNN
- ChebNet, GCN, MoNet, SplineCNN, FeaStNet
- Easy to get the famous sample data and transform same data format
- ModelNet, ShapeNet, etc.
- Many example and benchmark
■Accuracy
Accuracy (Classification)
- around 90% in any method (except VoxNet)

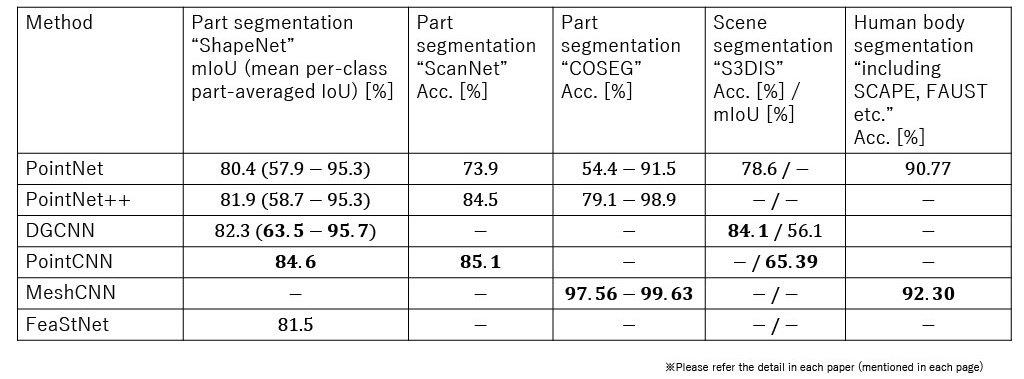
Accuracy (Segmentation)
■Dataset
3D Dataset
| Contents | Data Format | Purpose | PyTorch-geometric | |
|---|---|---|---|---|
| ModelNet10/40 | 3D CAD Model (10 or 40 classes) | Mesh (.OFF) | Classification | ModelNet |
| ShapeNet | 3D Shape | Point Cloud (.pts) | Segmentation | ShapeNet |
| ScanNet | Indoor Scan Data | Mesh (.ply) | Segmentation | – |
| S3DIS(original ,h5) | Indoor Scan Data | Point Cloud | Segmentation | S3DIS |
| SHREC | many type for each contest | – | Retrieval | – |
| SHREC2016 | Animal, Human (Part Data) | Mesh (.OFF) | Correspondence | SHREC2016 |
| TOSCA | Animal, Human | Mesh (same #vertices at each category, separate file of vertices and triangles) | Correspondence | TOSCA |
| PCPNet | 3D Shape | Point Cloud (.xyz) (Including normal, curvature files.) | Estimation of local shape (Normal, curvature) | PCPNet |
| FAUST | Human body | Mesh | Correspondence | FAUST |
ScanNet:registration required
S3DIS : registration required (for original)
FAUST(Note) : registration required
■Material
Material of 3D deep learning (3D / point cloud)
| Paper | Comment |
|---|---|
| A survey on Deep Learning Advances on Different 3D Data Representations | ・Review of 3D Deep Learning ・Easier to read it ・Written from point of view about Euclidean and Non-Euclidean method |
| Paperswithcode | ・Paper w/ code about 3D |
| Point Cloud Deep Learning Survey Ver. 2 | ・Deep learning for point cloud ・Survey of many papers |
Material of 3D deep learning (graph)
| Paper | Comment |
|---|---|
| Geometric deep learning: going beyond Euclidean data | Review of geometric deep learning |
| Geometric deep learning | summary of paper and code about geometric deep learning |
| Geometric deep learning on Graphs and Manifolds(NIPS2017) | Presentation (youtube) about geometric deep learning |
■Summary
There are many methods of 3D deep learning.
Two main method
- Euclidean vs Non-Euclidean
- Euclidean Method
- Projections / Multi-View / Voxel
- Non-Euclidean Method
- Point Cloud / Mesh / Graph
Each method have merit and demerit.
- We need to choose the better method for each data type and application.
The research about 3D deep learning is growing.
■Appendix
Appendix
- Mesh Generation
- Laplacian on Graph
- Correspondence
■Appendix : Mesh Generation
Mesh Generation
- In this material, I have summarized these materials.
| Link | Contents |
|---|---|
| 点群面張り(精密工学会) | Surface reconstruction |
| メッシュ処理(精密工学会) | Mesh processing |
| CV勉強会@関東発表資料 点群再構成に関するサーベイ | Survey of point cloud reconstruction |
Difficulty of Mesh Generation
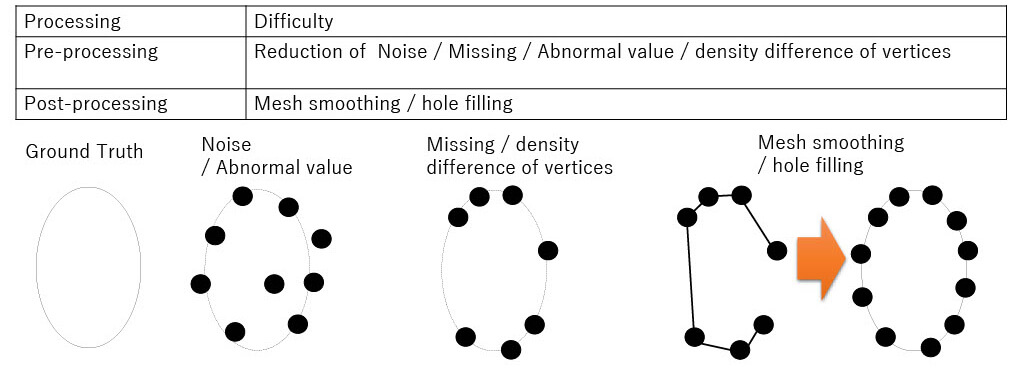
Kinds of Mesh Generation

Classification of the method
In general, it is easier to use the implicit method, since there are noise of point cloud.

Kinds of Mesh Generation (Detail)
Direct Triangulation (example of built-in function in MeshLab)
| Method | Feature |
|---|---|
| Voronoi-Based Surface Reconstruction | Creation of Delaunay diagram adding the vertices using Voronoi diagram |
| Ball-Pivoting Algorithm | Roll the ball over the point cloud and generate mesh from the point cloud located within a certain distance |
Voronoi-Based Surface Reconstruction
Voronoi diagram
- Region divided by the bisector of each vertices (in 2D)
Delaunay triangulation
- riangulation by connection of vertices

Ball-Pivoting Algorithm
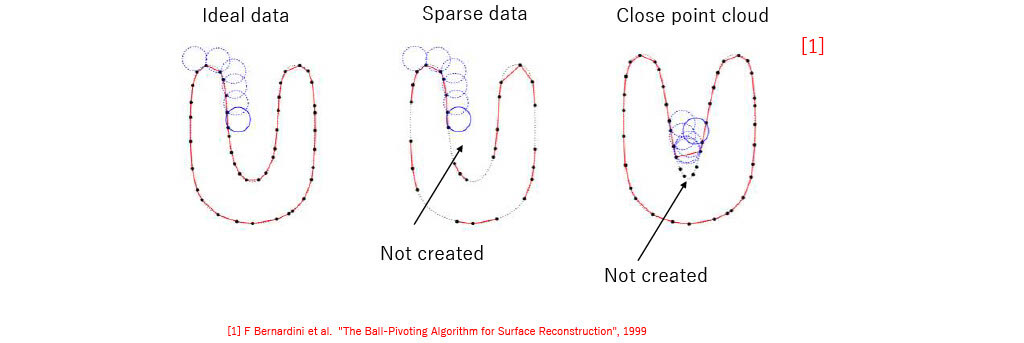
Kinds of Mesh Generation (Detail)
Surface Smoothness (example of built-in function in MeshLab)
| Method | Feature |
|---|---|
| Signed distance function + Marching Cubes | Creation of Signed distance function by using the distance b/w vertices and surface + Mesh generation by using Marching Cubes |
| Screened Poisson surface reconstruction (Poisson surface reconstruction) | Distinguish b/w inside and outside of surface by using Poisson eq. |
Signed distance function + Marching Cubes
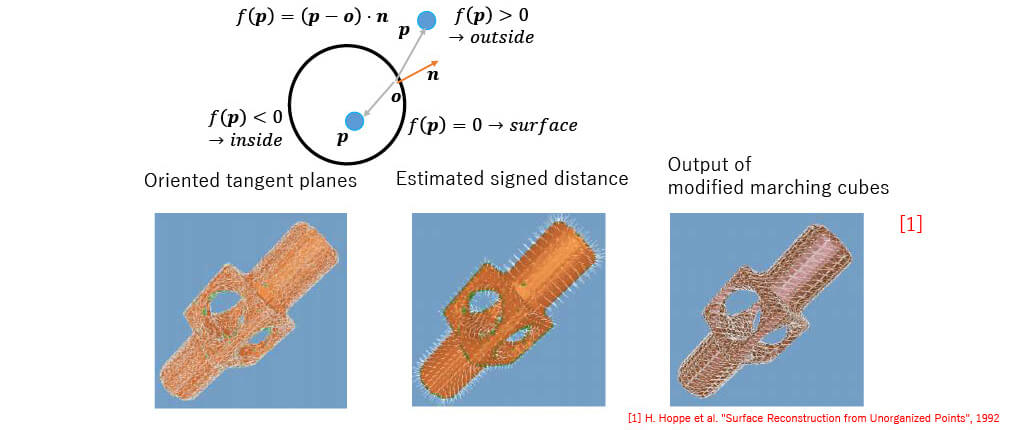
Screened Poisson surface reconstruction
get Indicator Function by solving the Poisson eq.

■Appendix : Laplacian on Graph
Laplacian on Graph [1]


Convolution

■Appendix :Correspondence
Correspondence [1]
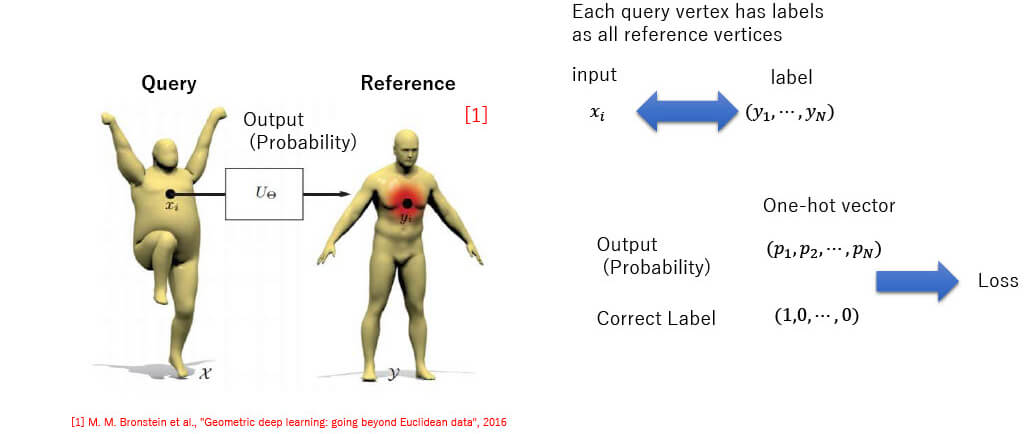
 ArithmerBlog
ArithmerBlog